Results

The step-detection algorithm used in this study used a peak detection method to detect steps through the variance in accelerometer reading. Vector of the dynamic body acceleration (VeDBA), a metric derived from tri-axial acceleration, was processed and analysed using the peak detection method to detect steps. The parameters for the algorithms were set after analysing a small subset of data from each session. 

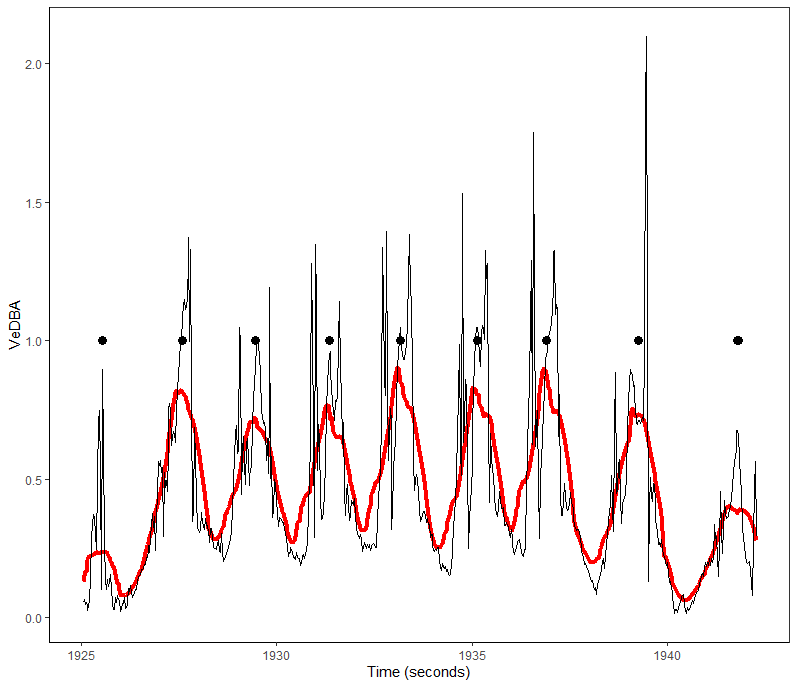
An 18-second subset of the data demonstrating the steps detected along the VeDBA during test session 1. “Event number” on the X-axis is the sequential data points logged by the Daily Diary tag. The black line represents the raw VeDBA calculated using Equation 1. The red line represents the VeDBA data after being smoothed by a factor of 35. The black dots represent the detected steps in the data.

4.1 Percent accuracy

The total number of steps, both defined and observed from the trained-walk and free-walk period of the test sessions, as well as the percent accuracy for each session is summarised in the table below.

SessionObserved stepsDefined stepsDifferencePercent accuracy
12032030100.0
295110186793.0
3104511207592.8
48929051398.5
56626892795.9
 Note The ‘observed’ steps are obtained from video analysis while the ‘defined’ steps are obtained from the algorithm through DDMT. The difference of steps was calculated using (defined steps – observed steps). The percent accuracy is calculated using the formula mentioned in the methods (Equation 2).

The percent accuracy for each session was calculated separately. The lowest accuracy was observed for session 3 at 92.8% and the highest accuracy was observed for session 1 at 100%. The average percent accuracy for the algorithm was found to be 96.0%.

4.2 VeDBA analysis

I compared the mean VeDBA between the three enclosures – indoor, big outdoor, and small outdoor enclosures. A Shapiro-Wilk test revealed that the data was not normally distributed (p<0.05). Thus, a Kruskal-Wallis test was performed.

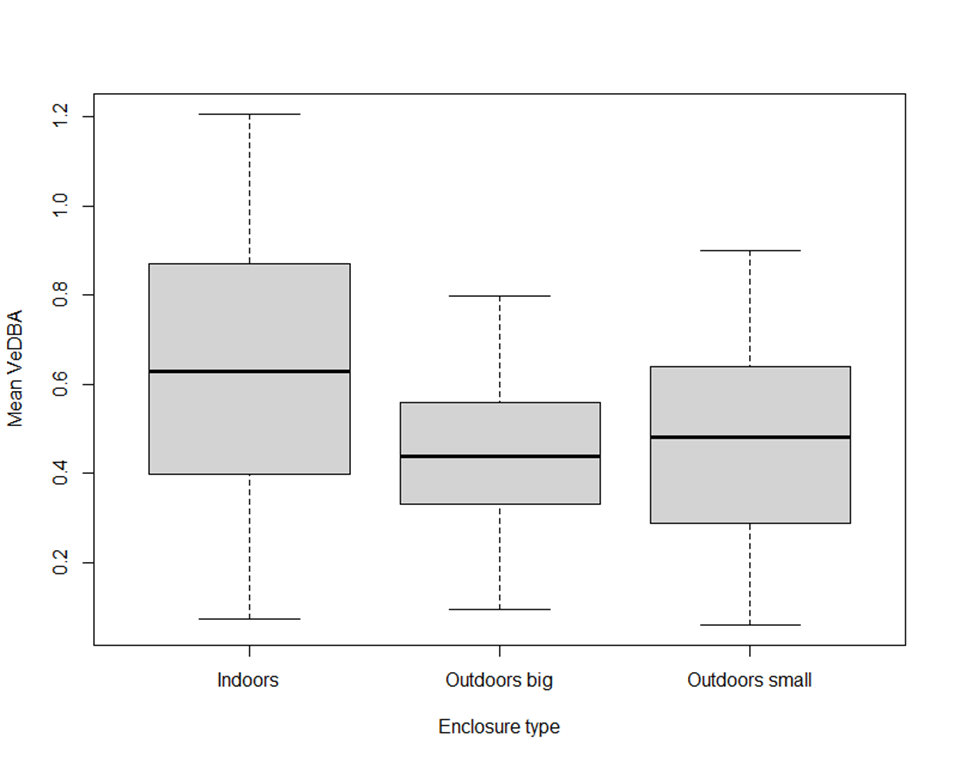
Mean VeDBA of the steps taken by Saonoi from three 15-minute data subsets from each enclosure, extracted from session 2. The VeDBA in the indoor enclosure was significantly different from the other two groups (p<0.001).

The number of steps was used as the sample size for the three subsets. The Kruskal-Wallis test (Kruskal-Wallis chi-squared = 25.36, p<0.001, df = 2) revealed that the mean VeDBA measures significantly differed between the three groups – indoor enclosure (0.625 + 0.284, n = 130), large outdoor enclosure (0.439 + 0.171, n = 60), and small outdoor enclosure (0.474 + 0.222, n = 107). The post HOC Dunn test showed a significant difference in the mean VeDBA between the indoor enclosure and big outdoor enclosure (p<0.001) as well as between the indoor and small outdoor enclosure (p<0.001), but not between the two outdoor enclosures (p = 0.986).

Let’s find out the implications of this study! Onwards to Discussion.